Целью рассмотрения данного
вопроса является построение однофакторной регрессионной модели, которая
наиболее точно выражает сущность исследуемой зависимости. Процесс
построения однофакторной регрессионной модели включает в себя следующие этапы:
1.
Подбор соответствующего типа математической зависимости, которая
наилучшим образом отражает характер изучаемой связи (линейная, нелинейная).
Этот этап играет важную роль
в корреляционном анализе, потому что от правильного выбора уравнения регрессии
зависит результат решения задачи.
Тип зависимости определяется с
помощью построения диаграмм рассеяния, рис. 3.1:
 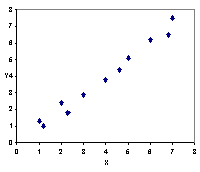 
Рисунок 3.1 - Диаграммы рассеяния
По виду скопления точек можно
выдвинуть гипотезу о форме зависимости между переменными.
Линейная зависимость между двумя
показателями характеризуется уравнением прямой:
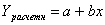 (3.11) (3.11)
где х – факторный показатель;
Yрасчетн
– результативный показатель;
a и b –
параметры уравнения регрессии, которые требуется отыскать.
Это уравнение описывает такую
связь между двумя признаками, при которой с изменением факторного показателя на
определенную величину наблюдается равномерное возрастание или убывание значений
результативного показателя.
Нелинейная зависимость может
характеризоваться:
– Параболой второго порядка: Yрасчетн = a + bx + cx2;
– Гиперболой: Yрасчетн = a + b/x и
т.п.
2.
Расчет параметров уравнения регрессии методом наименьших квадратов
(МНК), т.е. 
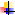 В
случае линейной зависимости имеем: В
случае линейной зависимости имеем:
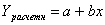 , , 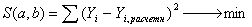
имеем: 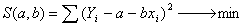
Функция будет принимать
минимальное значение, когда частные производные будут равны нулю:


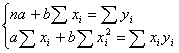 отсюда находим a
и b. отсюда находим a
и b.
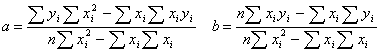 (3.12) (3.12)
 В
случае параболы второго порядка Yрасчетн
= a + bx + cx2 имеем: В
случае параболы второго порядка Yрасчетн
= a + bx + cx2 имеем:
 , , 
то есть 
Функция будет принимать
минимальное значение, когда частные производные будут равны нулю:


отсюда находим a,
b и с.
 В
случае гиперболы Yрасчетн = a + b/x имеем: В
случае гиперболы Yрасчетн = a + b/x имеем:
 , , 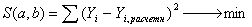
то есть 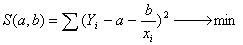
Функция будет принимать
минимальное значение, когда частные производные будут равны нулю:

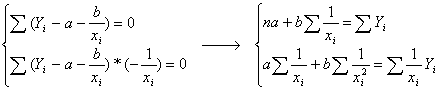
отсюда находим a
и b.
|