Процесс построения
многофакторной регрессионной модели включает в себя следующие этапы:
1. Подбор соответствующего типа
математической зависимости, которая наилучшим образом отражает характер
изучаемой связи (линейная, нелинейная).
При моделировании связи между
факторными и результативными показателями в случае множественной регрессии при
подборе уравнения, которое наилучшим образом описывает изучаемые зависимости,
также выполняют построение диаграмм рассеяния.
Различают:
– Линейную зависимость. Если
связь всех факторных показателей с результативным носит прямолинейный характер,
то для записей этих зависимостей можно использовать линейную функцию вида:
 (3.13)
– Степенную зависимость. Если
связь между результативным и факторным показателями носит криволинейный
характер, то может быть использована степенная функция вида:
 (3.14)
Логарифмируя данное выражение, приходим
к линейной функции:
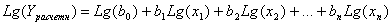
Для удобства вычислений и в
первом и во втором случае вводят фиктивную переменную x0=1.
С учетом этого уравнение линейной множественной регрессии представляется в
виде:
 , либо
 (3.15)
В случаях, когда трудно
обосновать форму зависимости, решение задачи можно провести по различным
моделям и сравнить полученные результаты. Адекватность моделей определяется по
критерию Фишера.
2. Расчет параметров уравнения регрессии
методом наименьших квадратов (МНК).
Все компоненты уравнения
регрессии представляются в виде соответствующих матриц (для линейной
регрессии):
 ,  , 
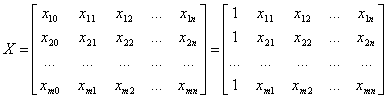Параметры уравнения регрессии рассчитываются
по формуле:
 (3.16)
Параметры уравнения регрессии
вида можно
найти используя функцию Microsoft Excel ЛИНЕЙН. Для этого
необходимо выполнить шаги:
– Отметить блок ячеек, где
должны находиться отчетные данные. Ширина блока – число оцениваемых параметров
(n+1), высота – 5 строк.
– Вызвать функцию ЛИНЕЙН:
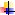1 аргумент – столбец Y;
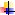2 аргумент – матрица [X];
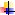3, 4 аргументы – истина.
– нажать
<F2>, <CTRL>+<SHIFT>+<ENTER>
Появится таблица 3.1:
Таблица
3.1
| 
