Все явления и процессы
хозяйственной деятельности предприятий находятся во взаимосвязи:
взаимозависимости и обусловленности. Одни из них непосредственно связаны между
собой, другие – косвенно. Каждый результативный показатель зависит от
многочисленных факторов. Чем детальнее исследуется влияние факторов на величину
результативного показателя, тем точнее результаты анализа.
Без глубокого и всестороннего
изучения факторов нельзя сделать обоснованные выводы о результатах
деятельности, выявить резервы производственной деятельности, обосновать планы и
управленческие решения.
Факторный анализ – методика
комплексного и системного изучения и измерения воздействия факторов на величину
результативных показателей.
Например, размер прибыли от
операционной деятельности зависит от объема и структуры продаж, цены и
себестоимости единицы продукции.
Типы факторного анализа:
– Детерминированный факторный
анализ – методика исследования влияния факторов, связь которых с результативным
показателем носит функциональный характер.
– Стохастический факторный
анализ – методика исследования влияния факторов, связь которых с результативным
показателем, в отличие от функциональной, является вероятностной
(корреляционной).
Например, производительность
труда при одном и том же уровне фондовооруженности на разных предприятиях может
быть неодинаковой. Однако, при увеличении уровня фондовооруженности,
сохраняется общая тенденция роста производительности труда.
Задачи факторного анализа:
1.
Отбор факторов для анализа исследуемых результативных показателей и их
классификация.
2.
Определение формы зависимости между факторными и результативными
показателями, построение факторной модели.
3.
Расчет влияния факторов и оценка роли каждого из них в изменении
величины результативного показателя.
Самой главной задачей
детерминированного факторного анализа является расчет влияния факторов на
величину результативных показателей, для чего в анализе используется целый
арсенал методов, сущность, назначение, сфера применения которых рассматривается
ниже.
Важно различать факторы по их
содержанию: экстенсивные (количественные), интенсивные (качественные); и по
уровню соподчиненности.
Некоторые факторы оказывают
непосредственное влияние на результативный показатель, другие – косвенное. По
уровню соподчиненности (иерархии) различают факторы первого, второго, третьего
и последующих уровней подчинения.
К факторам первого уровня
относятся те, которые непосредственно влияют на результативный показатель.
Факторы, которые определяют результативный показатель косвенно, при помощи
факторов первого уровня, называются факторами второго уровня и т.д.
Пример. Объем валовой
продукции промышленного предприятия представляется в виде произведения двух
факторов первого порядка: среднего количества рабочих и среднегодовой выработки
продукции одним рабочим, которая в свою очередь зависит от факторов второго
уровня, рис. 2.1:
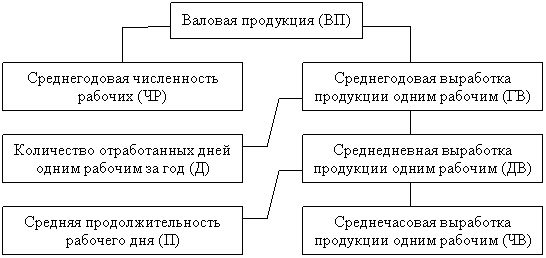
Рисунок 2.1 - Детерминированная факторная модель
Валовой продукции
Развитие детерминированной
факторной системы достигается, как правило, за счет детализации комплексных
(сложных) факторов. Элементные факторы не раскладываются на сомножители, так
как по своему содержанию они однородны. В нашем примере это: ЧР, Д, П. С
развитием системы комплексные факторы постепенно детализируются на менее общие,
постепенно приближаясь по своему аналитическому содержанию к элементным.
Однако необходимо заметить,
что развитие факторных систем на большую глубину связано с методологическими
трудностями, возникающими при анализе их влияния на результативный показатель.
Построить факторную модель – это
значит представить изучаемое явление в виде алгебраической суммы, частного или
произведения нескольких факторов, определяющих его величину.
Типы факторных моделей
детерминированного анализа:
1. Аддитивные модели.
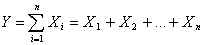 (2.1) (2.1)
Используются в тех случаях,
когда результативный показатель представляет собой алгебраическую сумму
нескольких факторных показателей. Расширение модели осуществляется за счет
расчленения одного или нескольких факторных показателей на составные
элементы-слагаемые:
Пусть A=B+C. Тогда если B=D+E-F, то A= D+E-F+C.
2. Мультипликативные модели.
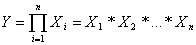 (2.2) (2.2)
Применяются, когда
результативный показатель представляет собой произведение нескольких факторов.
Преобразование модели
осуществляется путем последовательного расчленения факторов исходной системы на
факторы-сомножители (рис. 2.1):
ВП=ЧР*ГВ=ЧР*Д*ДВ=ЧР*Д*П*ЧВ
3. Кратные модели.
 (2.3) (2.3)
Применяются, когда
результативный показатель получают делением одного факторного показателя на
величину другого.
Способы преобразования:
– Удлинение числителя исходной
модели путем замены фактора на сумму однородных показателей:
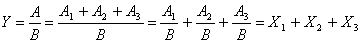 (2.4) (2.4)
– Формальное разложение –
удлинение знаменателя исходной факторной модели путем замены фактора на сумму
или произведение однородных показателей:
 или или 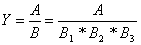 (2.5) (2.5)
– Расширение исходной факторной
модели за счет умножения и числителя и знаменателя на 1 или несколько
показателей:
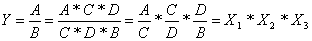 (2.6) (2.6)
– Сокращение – деление и
числителя и знаменателя исходной факторной модели на один и тот же показатель:
 (2.7) (2.7)
4. Смешанные (комбинированные)
модели – сочетание предыдущих моделей в различных комбинациях.
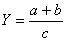 ; ; 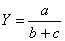 ; ;  ; ; 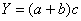 и т.д. (2.8) и т.д. (2.8)
Пример. Фондоотдача (ФО)
определяется отношением валовой продукции (ВП) к среднегодовой стоимости
основных производственных фондов (ОПФ). Разделив числитель и знаменатель на
среднегодовую численность рабочих (ЧР), получим модель с другими факторными
показателями: среднегодовой выработкой продукции одним рабочим (ГВ),
характеризующей уровень производительности труда, и фондовооруженности труда
(ФВ):
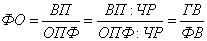 (2.9) (2.9)
В общем случае результативные
показатели могут быть разложены на факторы различными способами
(комбинированными). Выбор типа детерминированной факторной модели и способа ее
преобразования зависит от объекта исследования и поставленных задач.
|